Struktur Dasar dan Notasi Algoritma

STRUKTUR DASAR DAN NOTASI ALGORITMA

Algoritma berupa langkah-langkah penyelesaian suatu masalah/tugas. Langkah-langkah tersebut dapat berupa :

1. Runtunan (Sequence)
2. Pimilihan (Selection)
3. Pengulangan (Repetition)

Notasi Algoritmik bukan notasi bahasa pemrograman sehingga siapapun dapat membuat notasi algoritmik yang berbeda. Namun demikian ketaatan atas notasi perlu diperhatikan untuk menghindari kekeliruan.

Beberapa notasi yang digunakan untuk menulis algoritma :

a.       Untaian kalimat deskriptif

       Setiap langkah dinyatakan dengan bahasa yang gamblang/jelas

b.      Menggunakan diagram alir (flow chart)

c.       Menggunakan pseudo-code

Pseudo : semu, tidak sebenarnya, pura-pura; adalah notasi yang menyerupai notasi bahasa pemrograman tingkat tinggi

Suatu algoritma yang ditulis menggunakan diagram alir menggunakan simbol-simbol sebagai berikut :

Penulisan algoritma menggunakan pseudo code dapat menggunakan notasi-notasi sebagai berikut : 

Pernyataan	Notasi algoritmik	Maksud
Penulisan	write(x)	Nilai x dicetak di piranti keluaran
	write(x,y)	Nilai x dan y dicetak di piranti keluaran
	write(“Hello”)	Text Hello dicetak di piranti keluaran
Pembacaan	read(a)	Baca nilai a
	read(a,b)	Baca nilai a,b
Penugasan	bil¬x	Isikan nilai variabel x kedalam variabel bil

Teks algoritma (pseudo-code) terdiri dari :

Ø  Head(Judul) : memberikan nama pada algoritma; umumnya nama sudah dapat memberi gambaran pada prosedur penyelesaian masalah atau masalah yang akan diselesaikan

Ø  Deklarasi : menyatakan jenis dari setiap elemen data (variabel) yang akan digunakan dalam algoritma.

Ø  Deskripsi : merupakan inti prosedur penyelesaian masalah; meliputi pernyataan/ operasi, fungsi, penjelasan, dll.

CONTOH ALGORITMA :

a.Untaian kalimat deskriftif

ALGORITMA  Penjumlahan

Diberikan dua buah bilangan bulat positif A dan B. Algoritma Penjumlahan menjumlahakan nilai dua variabel A dan B, hasilnya disimpan pada variabel C

DESKRIPSI :

1. Baca nilai A dan B

2. Jumlahkan A dengan B, hasilnya berikan ke C

3. Cetak C

b. Flow Chart	c. Pseudo-code
	ALGORITMA Eucledian Program mencari pbt, m dan n bil bulat positif DEKLARASI : A, B : integer {input} C     : integer {hasil} DESKRIPSI : read(A,B)     C ← A + B  write(C)

Metode Sorting Menggunakan Selection Sort (contoh Script dalam bahasa C++)

SELECTION SORT

Selection sort merupakan kombinasi antara sorting dan searching. Pengertian dari selection sort adalah mencari elemen yang tepat untuk diletakkan di posisi yang telah diketahui, dan meletakkannya di posisi tersebut setelah data tersebut ditemukan.

Selection Sort Membandingkan elemen yang sekarang dengan elemen yang berikutnya sampai dengan elemen yang terakhir. Jika ditemukan elemen lain yang lebih kecil dari elemen sekarang maka dicatat posisinya dan kemudian ditukar.

Pengurutan data dalam struktur data sangat penting untuk data yang bertipe data numerik ataupun karakter. Pengurutan dapat dilakukan secara ascending (urut naik) dan descending (urut turun) Pengurutan (Sorting) adalah proses menyusun kembali data yang sebelumnya telah disusun dengan suatu pola tertentu, sehingga tersusun secara teratur menurut aturan tertentu.

Contoh:

Data Acak      : 5 6 8 1 3 25 10

Ascending      : 1 3 5 6 8 10 25

Descending    : 25 10 8 6 5 3 1

Konsep Algoritma pengurutan sederhana salah satunya adalah Selection Sort. Ide dasarnya adalah melakukan beberapa kali pass untuk melakukan penyeleksian elemen struktur data. Untuk sorting ascending (menaik),

elemen yang paling kecil di antara elemen-elemen yang belum urut, disimpan indeksnya, kemudian dilakukan pertukaran nilai elemen dengan indeks yang disimpan tersebut dengan elemen yang paling depan yang belum urut. Sebaliknya, untuk sorting descending (menurun), elemen yang paling besar yang disimpan indeksnya kemudian ditukar.

Selection Sort diakui karena kesederhanaan algoritmanya dan performanya lebih bagus daripada algoritma lain yang lebih rumit dalam situasi tertentu. Algoritma ini bekerja sebagai berikut:

1.        Mencari nilai minimum (jika ascending) atau maksimum (jika descending) dalam sebuah list.

2.        Menukarkan nilai ini dengan elemen pertama list.

3.        Mengulangi langkah di atas untuk sisa list dengan dimulai pada posisi kedua. Secara efisien kita membagi list menjadi dua bagian yaitu bagian yang sudah diurutkan, yang didapat dengan membangun dari kiri ke kanan dan dilakukan pada saat awal, dan bagian list yang elemennya akan diurutkan.

Cara mudahnya dalam mengurutkan selection sort :

1. Cek seluruh elemen array, temukan nilai terkecil jika assending dan sebaliknya jiaka dessendingkemudian tukarkan posisinya dengan posisi nilai yang tersimpan pada posisi pertama dari array.

2.  Temukan nilai terkecil/terbesar kedua dan tukarkan posisinya dengan nilai yang berada pada posisi kedua.

3. Elemen sebelumnya/dua elemen pertama tidak akan berubah lagi sebab mereka sudah merupakan nilai terkecil/terbesar pertama dan kedua dalam array tersebut, ulangi dengan cara/proses “pilih dan tukar” sampai semua elemen tersorting.

Metode selection sort:

Contoh Program Selection Sort

#include <iostream>

#include <conio.h>

using namespace std;

int data[10],data2[10];

int n;

void tukar(int a, int b)

{

 int t;

 t = data[b];

 data[b] = data[a];

 data[a] = t;

}

void selection_sort()

{

 int pos,i,j;

 for(i=0;i<n-1;i++)

 {

  pos = i;

  for(j = i+1;j<n;j++)

  {

   if(data[j] < data[pos]) pos = j;

  }

   if(pos != i) tukar(pos,i);

 }

}

main()

{

 cout<<"===PROGRAM SELECTION SORT==="<<endl;

 cout<<"Masukkan Jumlah Data : ";cin>>n;

 for(int i=0;i<n;i++)

 {

  cout<<"\nMasukkan data index ke [ "<<i<<" ]: ";cin>>data[i];

  data2[i]=data[i];

 }

 selection_sort();

 cout<<"\n\n";

 cout<<"Data Setelah di Sort : ";

 for(int i=0; i<n; i++)

 {

  cout<<" "<<data[i];

 }

 getch();

}

Metode Sorting Menggunakan Merge Sort (contoh Script dalam bahasa C++)

MERGE SORT

Metode pengurutan merge sort adalah metode pengurutan lanjut, sama dengan metode Quick Sort. Metode ini juga menggunakan konsep devideand conquer yang membagi data S dalam dua kelompok yaitu S1 dan S2 yang tidak beririsan (disjoint). Proses pembagian data dilakukan secara rekursif sampai data tidak dapat dibagi lagi atau dengan kata lain datadalam sub bagian menjadi tunggal. 

Setelah data tidak dapat dibagi lagi, proses penggabungan (merging) dilakukan antara sub-sub bagian dengan memperhatikan urutan data yang diinginkan (ascending/kecil ke besar atau descending/besar ke kecil). Proses penggabungan ini dilakukan sampai semua data tergabung dan terurut sesuai urutan yang diiginkan. Kompleksitas algoritma merge sort adalah O(n log n).

Cara kerja Merge Sort

Merge Sort adalah membagi larik data yang diberikan menjadi dua bagian yang lebih kecil. Kedua larik yang baru tersebut kemudian akan diurutkan secara terpisah. Setelah kedua buah list tersusun, maka akan dibentuk larik baru sebagai hasil penggabungan dari dua buah larik sebelumnya.

Ilustrasi Algoritma Merge Sort

Contoh Program

#include <stdio.h>

#define MAX 5

int Data[MAX];

int temp[MAX];

void merge(int Data[], int temp[], int kiri, int tengah, int kanan)

{

   int i, left_end, num_elements, tmp_pos;

   left_end = tengah - 1;

   tmp_pos = kiri;

   num_elements = kanan - kiri + 1;

   while ((kiri <= left_end) && (tengah <= kanan))

     {

        if (Data[kiri] <= Data[tengah])

        {

            temp[tmp_pos] = Data[kiri];

            tmp_pos = tmp_pos + 1;

            kiri = kiri +1;

        }

        else

        {

            temp[tmp_pos] = Data[tengah];

            tmp_pos = tmp_pos + 1;

            tengah = tengah + 1;

        }

      }

      while (kiri <= left_end)

      {

            temp[tmp_pos] = Data[kiri];

            kiri = kiri + 1;

            tmp_pos = tmp_pos + 1;

      }

      while (tengah <= kanan)

      {

            temp[tmp_pos] = Data[tengah];

            tengah = tengah + 1;

            tmp_pos = tmp_pos + 1;

      }

      for (i=0; i <= num_elements; i++)

      {

            Data[kanan] = temp[kanan];

            kanan = kanan - 1;

      }

}

void m_sort(int Data[], int temp[], int kiri, int kanan)

{

   int tengah;

   if (kanan > kiri)

   {

       tengah = (kanan + kiri) / 2;

       m_sort(Data, temp, kiri, tengah);

       m_sort(Data, temp, tengah+1, kanan);

       merge(Data, temp, kiri, tengah+1, kanan);

   }

}

void mergeSort(int Data[], int temp[], int array_size)

{

   m_sort(Data, temp, 0, array_size - 1);

}

int main()

{

   int i;

   printf("Masukkan DATA SEBELUM TERURUT : \n");

   for (i = 0; i < MAX; i++)

   {

      printf ("Data ke %i : ", i+1);

      scanf ("%d", &Data[i]);

   }

   mergeSort(Data, temp, MAX);

   printf("\nDATA SETELAH TERURUT : ");

   for (i = 0; i < MAX; i++)

   printf("%d  ", Data[i]);

   printf("\n");

   //scanf("%d");

   return(0);

}

Metode Sorting Menggunakan Quick Sort (contoh Script dalam bahasa C++)

Quick Sort

Algoritma quick sort diperkenalkan pertama kali oleh C.A.R. Hoare pada tahun 1960. Quick sort adalah algoritma sorting yang berdasarkan pembandingan dengan metode divide and conquer (bagi dan kuasai).

Disebut Quick Sort, karena Algoritma quick sort mengurutkan dengan sangat cepat. Quick sort disebut juga dengan partition exchange sort, karena konsepnya membuat partisi-partisi, dan sorting dilakukan per partisi.

Algoritma quick sort mengurutkan dengan sangat cepat, namun algoritma ini sangat komplex dan diproses secara rekursif. Sangat memungkinkan untuk menulis algoritma yang lebih cepat untuk beberapa kasus khusus, namun untuk kasus umum, sampai saat ini tidak ada yang lebih cepat dibandingkan algoritma quick sort.

Pivot

Dalam algoritma quick sort, pemilihan pivot adalah hal yang menentukan apakah algoritma quick sort tersebut akan memberikan performa terbaik atau terburuk. Berikut beberapa cara pemilihan pivot :

1.      Pivot adalah elemen pertama, elemen terakhir, atau elemen tengah array. Cara ini hanya bagus jika elemen tabel tersusun secara acak, tetapi tidak bagus jika elemen tabel semula sudah terurut.

2.      Pivot dipilih secara acak dari salah satu elemen array, Cara ini baik, tetapi belum tentu maksimal, sebab memerlukan prosedur khusus untuk menentukan pivot secara acak.

3.      Pivot adalah elemen median tabel. Cara ini paling bagus, karena hasil partisi menghasilkan dua bagian tabel yang berukuran seimbang. Cara ini memberikan kompleksitas waktu yang minimum. Masalahnya, mencari median dari elemen tabel yang belum terurut adalah persoalan tersendiri.

Contoh :

Pada array dengan data :

6

2

9

5

4

1

7

3

8

Pada data tersebut akan di urutkan menggunakan metode quick sort , pada contoh akan menggunakan pivot dari titik tengah pada array menggunakan aritmatika :

pivot = (x+y)/2

pivot = (0+8)/2 = 4

·         pivotnya berada pada indeks ke-4 yaitu = 4

·         pada data awal x = adalah nilai paling kiri dalam indeks array yaitu ( 0 ), x akan memindai data dari sebelah kiri dan akan mencari data yang lebih besar / sama dengan pivot, jika x menemukan data yang lebih kecil dari pivot maka x akan bergeser ke kanan (x+1).

·         pada data awal y = adalah nilai paling kanan dalam indeks array yaitu ( 8 ),y akan memindai data dari sebelah kanan dan mencari data yang lebih kecil / sama dengan pivot, jika y menemukan data yang lebih besar dari pivot maka y akan bergeser ke kiri (y-1).

·         Jika x dan y menemukan data yang sesuai dengan syarat diatas maka posisi dari data tersebut akan ditukar .

Indeks :

        [0]        [1]           [2]          [3]            [4]          [5]          [6]         [7]         [8]

6

2

9

5

4

1

7

3

8

       x                                                                                                                      y

Langkah 1: (data x > pivot) maka x berhenti pada indeks[0], (data y > pivot) maka y akan berjalan kekiri (y-1).

6

2

9

5

4

1

7

3

8

       x                                                                                                      y

Langkah 2: x tetap pada indeks[0], (data y < pivot) maka y berhenti pada indeks[7] dan syarat terpenuhi maka data pada indeks [0] dan [7] ditukar, setelah posisi ditukar maka x bergeser ke kanan (x+1) dan y bergeser ke kiri (y-1).

3

2

9

5

4

1

7

6

8

                       x                                                                       y

Langkah 3: (data x < pivot) maka x bergeser ke kiri (x+1), (data y > pivot) maka y akan bergeser ke kanan (y-1).

3

2

9

5

4

1

7

6

8

                                      x                                          y

Langkah 4: (data x > pivot) maka x berhenti pada indeks[2], (data y < pivot) maka y berhenti pada indeks[5] dan syarat terpenuhi maka data pada indeks [2] dan [5] ditukar, setelah posisi ditukar maka x bergeser ke kanan (x+1) dan y bergeser ke kiri (y-1).

3

2

1

5

4

9

7

6

8

                                                       x           y

Langkah 5: (data x > pivot) maka x berhenti pada indeks [3], (data y = pivot) maka y berhenti pada indeks[4] dan syarat terpenuhi maka data pada indeks [3] dan [4] ditukar, setelah posisi ditukar maka x bergeser ke kanan (x+1) dan y bergeser ke kiri (y-1).

3

2

1

4

5

9

7

6

8

                                                      y             x

karena x > y maka pembagian partisi telah selesai dan array menjadi 2 bagian, seperti di bawah ini bagian kiri dari pivot akan berisi data yang lebih kecil dan sebelah kanan pivot akan berisi data yang lebih besar.

Maka sorting akan diteruskan dengan masing-masing partisi, yaitu partisi kiri terlebih dahulu dan kemudian partisi kanan.

        [0]        [1]           [2]          [3]            [4]          [5]          [6]         [7]         [8]

3

2

1

4

5

9

7

6

8

3

2

1

          x                            y                      

Langkah 6: pivot pada partisi kiri adalah (0+2)/2=1 maka pivotnya berada pada indeks[1] = 2, maka di cek (data x > pivot) maka x tetap pada indeks[0], (data y < pivot) dan syarat terpenuhi maka data pada indeks [0] dan [2] ditukar, setelah posisi ditukar maka x bergeser ke kanan (x+1=1) dan y bergeser ke kiri (y-1=1).

1

2

3

Maka nilai x=y dan sorting untuk partisi kiri selesai, maka akan dilanjutkan dengan partisi kanan.

        [0]        [1]           [2]          [3]            [4]          [5]          [6]         [7]         [8]

3

2

1

4

5

9

7

6

8

5

9

7

6

8

                                                                     x                                                   y

Langkah 7: pivot pada partisi kiri adalah (4+8)/2=6 maka pivotnya berada pada indeks[6] = 7, maka di cek (data x < pivot) maka x bergeser ke kanan (x+1), (data y > pivot) maka y bergeser ke kiri (y-1).

                                                                  [4]          [5]            [6]           [7]           [8]

5

9

7

6

8

                                                                                   x                               y

Langkah 8: (data x > pivot) maka x berhenti pada indeks [5], (data y = pivot) maka y berhenti pada indeks[7] dan syarat terpenuhi maka data pada indeks [5] dan [7] ditukar, setelah posisi ditukar maka x bergeser ke kanan (x+1=6) dan y bergeser ke kiri (y-1=6).

                                                                  [4]          [5]            [6]           [7]           [8]

5

6

7

9

8

            Maka x=y maka sorting pada partisi kanan selesai dan terbagi menjadi 2 bagian partisi :

                                                                            kanan 1                               kanan 2

5

6

9

8

                                                                    x          y                             

Langkah 9: pada partisi kanan 1 pivotnya adalah (4+5)/2=4,5 karena int tidak mengenal pecahan maka dibulatkan menjadi 4 , pivot = [4] = 5 kemudian di cek (data x = pivot) maka x tetap, di cek (data y > pivot) maka y mundur satu langkah menjadi y-1=5 sehingga nilai x=y sorting selesai tanpa adanya perubahan

9

8

                                                                                                                     x          y

Langkah 10: pada partisi kanan 2 pivotnya adalah (7+8)/2=7,5 karena int tidak mengenal pecahan maka dibulatkan menjadi 7 , pivot = [7] = 9, kemudian di cek (data x = pivot) maka x tetap pada indeks[7], (data y < pivot) dan syarat terpenuhi maka data pada indeks [7] dan [8] ditukar, setelah posisi ditukar maka x bergeser ke kanan (x+1=1) dan y bergeser ke kiri (y-1=1).

8

9

            karena x > y maka sorting selesai.

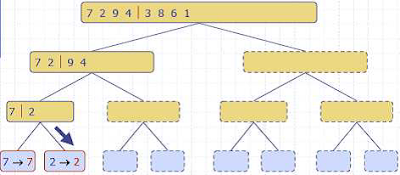
Untuk lebih jelasnya perhatikan gambar berikut ini :

        [0]        [1]           [2]          [3]            [4]          [5]          [6]         [7]         [8]

6

2

9

5

4

1

7

3

8

       x                                                                                                 y

6

2

9

5

4

1

7

3

8

       x                                                                                   y

3

2

9

5

4

1

7

6

8

                  x                                                             y

3

2

9

5

4

1

7

6

8

                               x                                   y

3

2

1

5

4

9

7

6

8

                                           x           y

3

2

1

4

5

9

7

6

8

3

2

1

5

9

7

6

8

       x                                y                                       x                                y

1

2

3

5

9

7

6

8

                                                                                                x=y

1

3

5

6

7

9

8

1

3

5

6

9

8

                                                                       x          y                               x           y

1

3

5

6

8

9

1

2

3

4

5

6

7

8

9

Berikut Program untuk Quick Sort :

#include <iostream>

#include <conio.h>

using namespace std;

void quick_sort(int arr[], int left, int right)

{

      int i = left, j = right;int tmp;

      int pivot = arr[(left+right)/2];/* partition */

                        while (i<j){

                                    while (arr[i] < pivot)

                                    i++;

                                    while (arr[j] > pivot)

                                    j--;

                                    if (i<=j){

                                                tmp = arr[i];

                                                arr[i] = arr[j];

                                                arr[j] = tmp;

                                                i++;j--;

                                                    };

                                          }; /* recursion */

      if (left < j)

            quick_sort(arr, left, j);

      if (i < right)

            quick_sort(arr, i, right);

}

int main()

{

int i,n,data[50];

cout<<"Masukan banyak data: ";cin>>n;

for(i=0;i<n;i++)

{cout<<"Masukan data ["<<i<<"] : ";cin>>data[i];}

cout<<"Data sebelum diurutkan: "<<endl;

for(i=0;i<n;i++)

{

cout<<data[i]<<" ";

}cout<<"\n";

quick_sort(data,0,n-1);//hasil pengurutan

cout<<"hasil pengurutan:\n";

{

int i;

for (i=0;i<n;i++)

cout<<data[i]<<" ";

cout<<"\n";

}getch();

}

jika kalian ingin dokumennya silahkan download disini : ACADEMIA